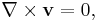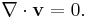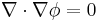Laplacian vector field

In vector calculus, a Laplacian vector field is a vector field which is both irrotational and incompressible. If the field is denoted as v, then it is described by the following differential equations:

$\nabla \times \mathbf{v} = 0,$

$\nabla \cdot \mathbf{v} = 0.$

A Laplacian vector field in the plane satisfies the Cauchy-Riemann equations: it is holomorphic.

Since the curl of v is zero, it follows that v can be expressed as the gradient of a scalar potential (see irrotational field) φ :

$\mathbf{v} = \nabla \phi \qquad \qquad (1)$ .

Then, since the divergence of v is also zero, it follows from equation (1) that

$\nabla \cdot \nabla \phi = 0$

which is equivalent to

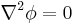$\nabla^2 \phi = 0$ .

Therefore, the potential of a Laplacian field satisfies Laplace's equation.

See also